 Dentro del bloque de análisis explicado en los cursos de bachillerato en la materia de matemáticas podemos encontrar el estudio de los intervalos de crecimiento de una función polinómica, así como el estudio de sus extremos relativos. A continuación se explica con un ejemplo los pasos a seguir utilizando el criterio de la primera derivada.
Dentro del bloque de análisis explicado en los cursos de bachillerato en la materia de matemáticas podemos encontrar el estudio de los intervalos de crecimiento de una función polinómica, así como el estudio de sus extremos relativos. A continuación se explica con un ejemplo los pasos a seguir utilizando el criterio de la primera derivada.
Función
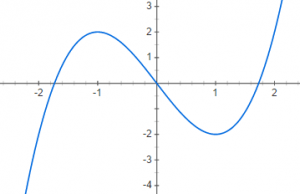
La función elegida para su análisis es la siguiente:
[latex]\huge \begin{matrix} f(x)=x^3-3x \end{matrix}[/latex]
Extremos relativos
Para estudiar tanto los extremos relativos como los intervalos de crecimiento deberemos de hallar la primera derivada. El valor de la primera derivada en un punto dado de dicha función (punto de abscisa x=a y ordenada y=b), coincide con la pendiente de la recta tangente a la función en ese punto. Como en los extremos relativos la pendiente de la recta tangente es cero, podemos afirmar que los extremos relativos se hallan en aquellos valores de x que hacen cero la primera derivada. El siguiente paso es igualar a cero la derivada obtenida y despejar la ecuación resultante.
[latex]\huge \begin{matrix} f'(x)=3x^2-3 \end{matrix}[/latex]
[latex]\huge \begin{matrix} 3x^2-3=0 \end{matrix}[/latex]
[latex]\huge \begin{matrix} x_{1}=-1\\ x_{2}=1 \end{matrix}[/latex]
Criterio de la primera derivada
Una vez hallados los extremos relativos (en esta función se encuentran en x=1 y x=-1) dividimos la recta de números reales en intervalos marcando dichos extremos relativos. Hallamos el signo de la primera derivada en cada uno de los intervalos:
Para el intervalo [latex](1,+\infty)[/latex], si hallamos f'(2)=9, la primera derivada es positiva, por lo que en este intervalo la función es creciente.
Para el intervalo [latex](-1,1)[/latex], si hallamos f'(0)=-3, la primera derivada es negativa, por lo que en este intervalo la función es decreciente.
Para el intervalo [latex](-\infty,-1 )[/latex], si hallamos f'(-2)=9, la primera derivada es positiva, por lo que en este intervalo la función es creciente.
De lo anterior se deduce que en x=-1 la función tiene un máximo relativo y en x=1 la función tiene un mínimo relativo.
Coordenadas de los extremos relativos
Por último, hallaremos las coordenadas de cada extremo relativo para su posterior representación gráfica:
Para x=1
[latex]\huge \begin{matrix} f(1)=1^3-3 \cdot 1 = -2 \end{matrix}[/latex]
[latex]\huge \begin{matrix} (1,-2) \end{matrix}[/latex]
Para x=-1
[latex]\huge \begin{matrix} f(-1)=(-1)^3-3 \cdot (-1) = 2 \end{matrix}[/latex]
[latex]\huge \begin{matrix} (-1,2) \end{matrix}[/latex]